Probabilidad Condicional

La probabilidad condicional es la probabilidad de algún evento A , dada la ocurrencia de algún otro evento B . Esto está denotado por P( A | B ) y se lee “la probabilidad de A , dado B ”.

En otras palabras, estamos calculando probabilidades condicionales al conocer información adicional parcialmente a través del experimento.

pueden darse dos tipos genéricos de situaciones:

Los sucesos son independientes entre sí, de manera que no influyen uno en el otro.

Cada suceso está condicionado por el resultado del anterior.

Cuando un suceso A influye en el resultado de un segundo suceso B, se dice que la probabilidad de éste es una probabilidad condicionada, expresado como P (B / A), cuyo valor es:

El suceso A no puede ser un suceso imposible, pues sería P (A) = 0

Ejemplo :

Una maestra de matemáticas le da a su clase dos exámenes. El 30% de la clase paso ambos exámenes y el 45% de la clase paso el primer examen. Qué porcentaje de aquellos que pasaron el primer examen también pasaron el segundo?

Dos tercios o aproximadamente el 66.7% de la clase paso el segundo examen.

El siguiente vídeo muestra como solucionar paso a paso un problema de probabilidad condicional.

TEOREMA DE BAYES

El teorema de Bayes es utilizado para calcular la probabilidad de un suceso, teniendo información de antemano sobre ese suceso.

Podemos calcular la probabilidad de un suceso A, sabiendo además que ese A cumple cierta característica que condiciona su probabilidad. El teorema de Bayes entiende que la probabilidad de forma inversa al teorema de la probabilidad total. El teorema de la probabilidad total hace inferencia sobre un suceso B, a partir de los resultados de los sucesos A. Por su parte, Bayes calcula la probabilidad de A condicionando a B

EJEMPLO:

Tenemos tres cajas con bombillas. La primera contiene 10 bombillas, de las cuales hay cuatro fundidas; en la segunda hay seis bombillas, y tan sólo una fundida, y en la tercera hay tres bombillas fundidas de un total de ocho. Si cogemos una bombilla fundida, ¿cuál es la probabilidad de que sea de la caja 1?

Recordemos que C1, C2, C3 representan las cajas 1, 2 y 3, también F= Bombilla fundida por lo que F¯ = Bombilla no fundida.

Ahora sólo nos interesa la rama superior de nuestro diagrama en árbol.

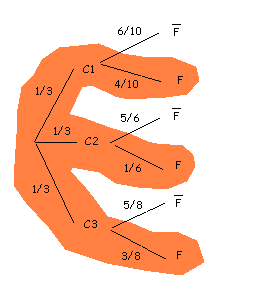
Nos interesa

. Por el teorema de Bayes,

En nuestro caso,

es decir, un

VIDEO:

Distribución de Poisson

La distribución de Poisson es una distribución de probabilidad discreta que se aplica a las ocurrencias de algún suceso durante un intervalo determinado. Nuestra variable aleatoria x representará el número de ocurrencias de un suceso en un intervalo determinado, el cual podrá ser tiempo, distancia, área, volumen o alguna otra unidad similar o derivada de éstas.

La probabilidad de nuestra variable aleatoria X viene dada por la siguiente expresión:

donde:

Nuestra variable aleatoria discreta puede tomar los valores:

donde es la media del número de sucesos en el intervalo que estemos tomando, ya sea de tiempo, distancia, volumen, etc. Es importante entender que este valor es una media en el sentido estrictamente estadístico de la palabra y como tal se calculará mediante dicha expresión y no debe calcularse nunca con una regla de proporcionalidad o regla de tres.

Se debe cumplir la condición de normalización

· La desviación típica es

· Cuando realizamos un experimento contando sucesos y obtenemos un valor x, su error vendrá determinado por la raíz de x.

La distribución de Poisson es discreta (como la binomial) pues los valores que puede tomar la variable aleatoria son números naturales. Aunque en la distribución de Poisson los casos posibles en teoría son infinitos (numerable).

La distribución de Poisson se caracteriza por un solo parámetro landa.

La función de densidad está definida así:

Su media es landa y su varianza también es landa:

La distribución de Poisson debe de cumplir los siguientes requisitos:

La variable discreta x es el número de ocurrencias de un suceso durante un intervalo.

Las ocurrencias deben ser aleatorias y no contener ningún vicio que favorezca unas ocurrencias en favor de otras.

Las ocurrencias deben estar uniformemente distribuidas dentro del intervalo que se emple.

EJEMPLOS

1.- Si ya se conocen que solo el 3% de los alumnos de contabilidad son muy inteligentes, ¿calcula la probabilidad de que si tomamos 100 alumnos al azar 5 de ellos sean muy inteligentes?

n= 100

P= 0.03

lambda = 100*0.03 = 3

x= 5

e= 2.718281828

P(X=5) = (e^-3)(3⁵)/5!= 0.10081

2.-Se calcula que en la ciudad el 20% de las personas tienen defecto de la vista, si tomamos una muestra de 50 personas al azar, ¿calcula la probabilidad de que 10 de ellos tengan defecto en la vista?

n= 50

p= 0.2

lambda= 10

P(X=10) = (e^-10)(10¹⁰)/10!= 0.12511

VIDEO COMPLEMENTARIO