Distribución normal
- Distribución normal o gaussiana. Función de densidad de probabilidad para la variable aleatoria continua.
- La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos
- La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal.
La función asociada a la distribución normal está dada por:
Donde: μ: media de la distribución.
σ: desviación estándar de la distribución.
π = 3.1416
x: variable aleatoria.
A una distribución normal de media μ y desviación estándar σ se le denota N(μ,σ).
La distribución normal cuando μ = 0 y σ = 1 recibe el nombre de curva normal unitaria (N(0,1)
Representación gráfica
La representación gráfica de esta distribución es una curva simétrica y su forma se asemeja a una campana por lo que se conoce como campana de Gauss
Propiedades de la distribución normal:
La distribución normal posee ciertas propiedades importantes que conviene destacar:
- Tiene una única moda, que coincide con su media y su mediana.
- La curva normal es asintótica al eje de abscisas. Por ello, cualquier valor entre
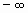y 
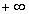es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1. - Es simétrica con respecto a su media
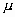. Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor. - La forma de la campana de Gauss depende de los parámetros
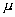y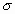 
. La media indica la posición de la campana, de modo que para diferentes valores de 
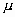la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de 
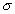, más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
Intervalos de una distribución normal
Tipificación de una variable
Es posible expresar cualquier distribución normal como una de la forma unitaria (N(0,1)), la cual se denomina distribución normal tipificada. Para ello se utiliza la expresión:
Una de las ventajas de tipificar una distribución es que se puede medir la desviación de los datos respecto a la media, lo cual permite comparar la posición relativa de los datos.
La distribución tipificada se aplica en estadística inferencial para determinar intervalos de confianza para la media de una población, usualmente se utiliza un nivel de confianza del 95% para el cual Z = 1.96.
EJEMPLO DE DISTRIBUCIÓN NORMAL
VÍDEO EXPLICATIVO
Vídeo ejercicio
FUENTES:
https://www.ecured.cu/Distribuci%C3%B3n_normal#Intervalos_de_una_distribuci.C3.B3n_normalhttps://www.fisterra.com/mbe/investiga/distr_normal/distr_normal.asp#Figura%203https://matemovil.com/wp-content/uploads/2018/06/Distribuci%C3%B3n-Normal-Ejercicios-Resueltos-PDF.pdfhttps://www.youtube.com/watch?v=phY8Z9-TXCYDistribución Binomial
La Distribución Binomial esta relacionada con al distribución de Bernoulli que es una distribución de variable aleatoria X que toma solamente valores de cero y uno (éxito y fracaso), cuando se realiza un solo experimento.
La distribución binomial se aplica cuando se realizan un número "n" de veces el experimento de Bernouilli, siendo cada ensayo independiente del anterior. La variable puede tomar valores entre 0 (si todos los experimentos han sido fracaso) y n (si todos los experimentos han sido éxitos)
Para este tipo de distribución de probabilidad, la función matemática es la siguiente:
n es el número de pruebas.
k es el número de éxitos.
p es la probabilidad de éxito.
q es la probabilidad de fracaso.
Condiciones
La distribución binomial es una distribución de probabilidades que surge al cumplirse las siguientes condiciones:
- El número de ensayos o repeticiones del experimento (n) es constante.
- En cada ensayo hay sólo dos posibles resultados (éxito o fracaso, defectuoso o no defectuoso).
- La probabilidad de cada resultado posible en cualquier ensayo permanece constante.
- En cada ensayo, los dos resultados posibles son mutuamente excluyentes.
- Los resultados de cada ensayo son independientes entre si.
EJEMPLOS:
Se lanza una moneda cuatro veces. Calcular la probabilidad de que salgan más caras que cruces
B(4, 0.5) p = 0.5q = 0.5
Otro ejemplo lo podemos observar en el siguiente video donde se nos explica paso a paso.
FUENTES:
ENSAYO DE BERNOULLI
Para empezar debemos saber que es un ensayo de bernoulli, este consiste en realizar
un solo experimento (ensayo) en el cual existen solo dos posibles resultados:
un solo experimento (ensayo) en el cual existen solo dos posibles resultados:
S = {éxito, fracaso}
P/E:
Observar un articulo y ver si es defectuoso
definimos a la variable aleatoria de bernoulli de la siguiente forma:
I = {0 si el resultado del ensayo es "fracaso"
I = {1 si el resultado del ensayo es "exitoso"
a esta ultima se le conoce como "función indicadora"
DISTRIBUCION DE BERNOULLI
Supongamos que en un ensayo de Bernoulli la probabilidad de obtener éxito es p.
Como el ensayo tiene únicamente de resultados posibles, entonces la probabilidad
de obtener un fracaso es 1–p. En donde llamaremos q a la probabilidad de fracaso.
Como el ensayo tiene únicamente de resultados posibles, entonces la probabilidad
de obtener un fracaso es 1–p. En donde llamaremos q a la probabilidad de fracaso.
p=Probabilidad de éxito
q=(1–p)=Probabilidad de fracaso
Con esto, la distribución de probabilidad de la variable aleatoria de Bernoulli es:
La media o valor esperado de la variable aleatoria de Bernoulli es:
E [ I ] = 0q + 1p = p µI = p
La varianza de la variable aleatoria de Bernoulli es:
V[I]= E[I2]−E[I]2
V[I]=(0q+1p)−p =p−p =p(1−p)=pq
σ2 =pq
Si llamamos X, en lugar de I, a la variable aleatoria de Bernoulli, su distribución de
la probabilidad queda:
La cual también se puede abreviar de la forma:
"Lanzar una moneda, probabilidad de conseguir que salga
cruz".Se trata de un solo experimento,
con dos resultados posibles: el éxito (p) se considerará sacar cruz. Valdrá 0,5. El fracaso (q)
que saliera cara, que vale (1 - p) = 1 - 0,5 = 0,5. La variable aleatoria X medirá "número de cruces
que salen en un lanzamiento", y sólo existirán dos resultados posibles: 0 (ninguna cruz, es decir,
salir cara) y 1 (una cruz).
con dos resultados posibles: el éxito (p) se considerará sacar cruz. Valdrá 0,5. El fracaso (q)
que saliera cara, que vale (1 - p) = 1 - 0,5 = 0,5. La variable aleatoria X medirá "número de cruces
que salen en un lanzamiento", y sólo existirán dos resultados posibles: 0 (ninguna cruz, es decir,
salir cara) y 1 (una cruz).
Por tanto, la v.a. X se distribuirá como una Bernoulli, ya
que cumple todos los
requisitos.
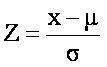
No hay comentarios:
Publicar un comentario